How to convert the horizontal and vertical components to east and north

This article describes how to convert the u (horizontal) and v (vertical) components from the ice motion data set to East and North components on the Earth's surface. Instructions for both the Northern and Southern Hemispheres are described below:

Northern Hemisphere

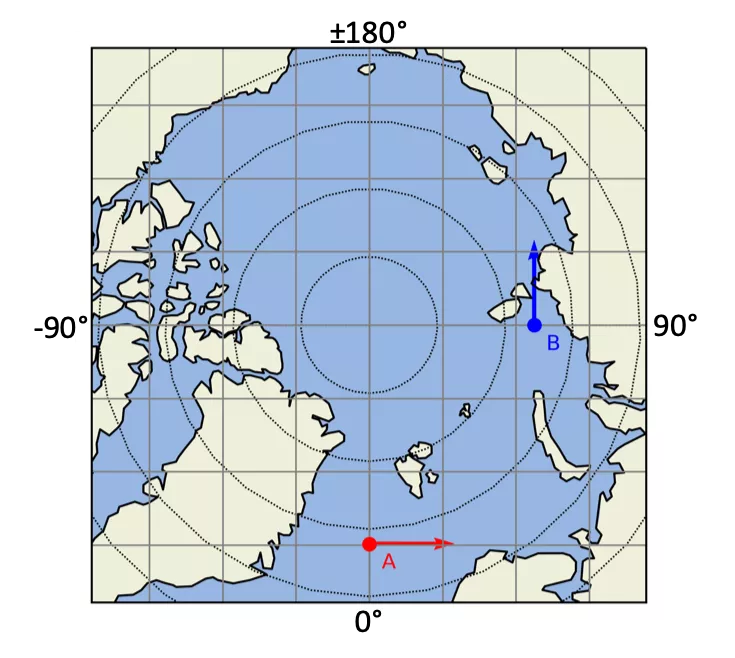
The latitudes and longitudes for the Northern Hemisphere are shown in Figure 1. 

Figure 1. Latitudes and longitudes for the Northern Hemisphere. 

The directions in the product are:

• u: toward the right on the grid
• v: upward (toward the top) on the grid
• East is counterclockwise
• North is toward the center of the grid

To compute the East and North components, apply a rotation matrix, which results in:

• E:   u * cos L  +  v * sin L
• N:  -u * sin L  +  v * cos L
  • where L is the longitude
  • Note the negative sign in the first term of N

 This can be checked by verifying that:

• at L=0o, a u-only vector (to the right) corresponds to east (positive E)
• at L=0o, a v-only vector (toward the top) corresponds to north (positive N)
• at L=90o, a u-only vector (to the right) corresponds to south (negative N)
• at L=90o, a v-only vector (toward the top) corresponds to east (positive E)

In Figure 1, both vectors A and B are pointing East.

Southern Hemisphere

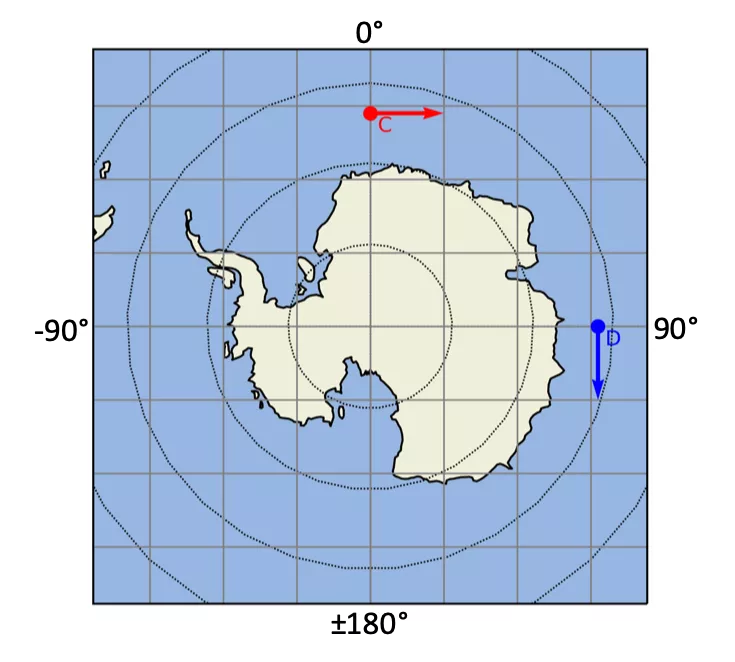
​The latitudes and longitudes for the Northern Hemisphere are shown in Figure 2. 

Figure 2. Latitudes and longitudes for the Southern Hemisphere. 

The directions in the data set are:

• u: toward the right on the grid
• v: upward (toward the top) on the grid
• East is clockwise
• North is outward from the center of the grid

To compute East and North components, apply a rotation matrix, which results in:

• E:   u * cos L  -  v * sin L
• N:   u * sin L  +  v * cos L
  • where L is the longitude
  • Note the negative sign in the second term of E

 This can be checked by verifying that:

• at L=0o, a u-only vector (to the right) corresponds to east (positive E)
• at L=0o, a v-only vector (toward the top) corresponds to north (positive N)
• at L=90o, a u-only vector (to the right) corresponds to north (positive N)
• at L=90o, a v-only vector (toward the top) corresponds to west (negative E)

In Figure 2, both vectors C and D are pointing East.